Universal audio synthesizer control with normalizing flows

This website is still under construction. We keep adding new results, so please come back later if you want more.

This website presents additional material and experiments around the paper Universal audio synthesizer control with normalizing flows.

The ubiquity of sound synthesizers has reshaped music production and even entirely defined new music genres. However, the increasing complexity and number of parameters in modern synthesizers make them harder to master. We thus need methods to easily create and explore with synthesizers.

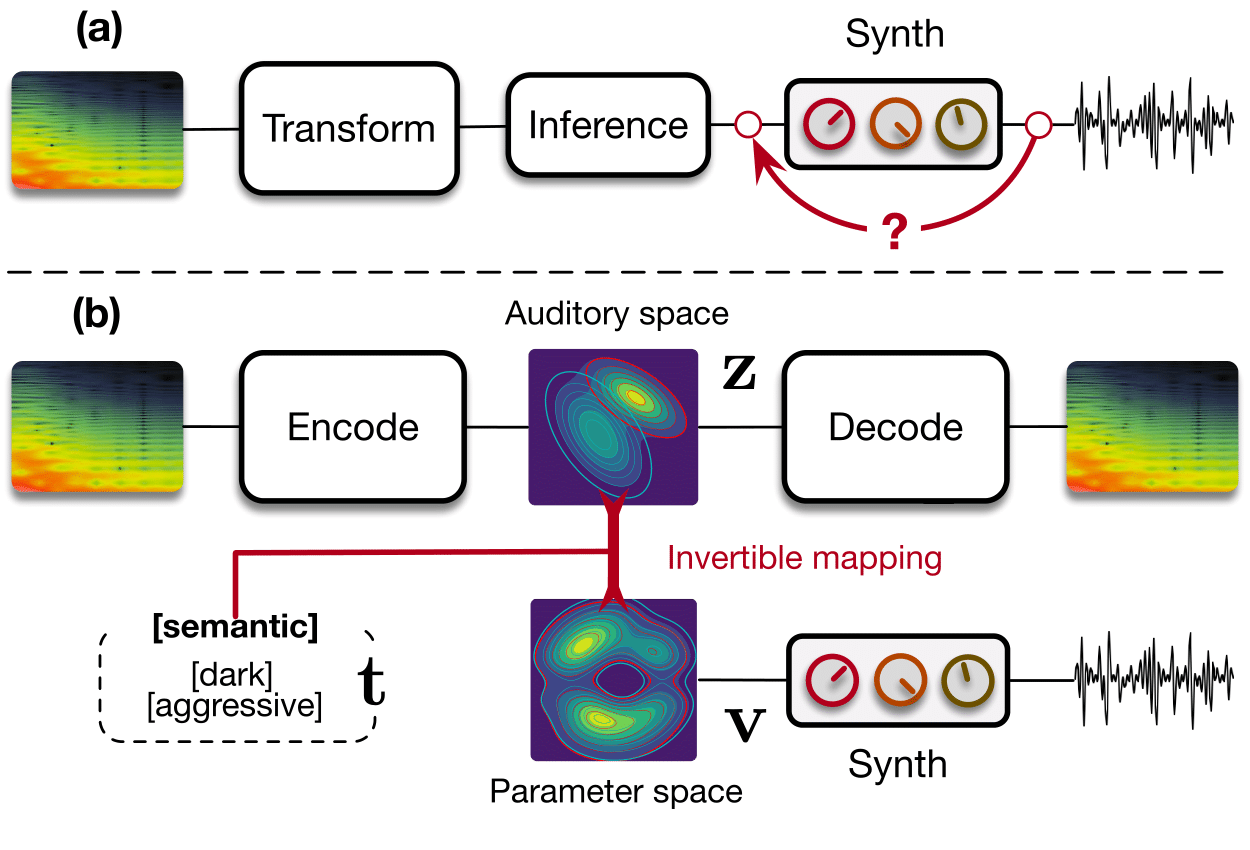
Our paper introduces a radically novel formulation of audio synthesizer control. We formalize it as finding an organized latent audio space that represents the capabilities of a synthesizer, while constructing an invertible mapping to the space of its parameters. By using this formulation, we show we can address simultaneously automatic parameter inference, macro-control learning and audio-based preset exploration within a single model. To solve this new formulation, we rely on Variational Auto-Encoders (VAE) and Normalizing Flows (NF) to organize and map the respective auditory and parameter spaces. We introduce a new type of NF named regression flows that allows to perform an invertible mapping between separate latent spaces, while steering the organization of some of the latent dimensions.

Contents

• Audio reconstruction
• Macro-control learning
• Audio space interpolation
• Vocal sketching
• Real-time implementation using Ableton Live
• Code

Audio reconstruction

Our first experiment consists in evaluating the reconstruction ability of our model. Reconstruction is done via parameter inference, which means an audio sample is embedded in the latent space, then mapped to synth parameters, that are used to synthesize the reconstructed audio. In the examples below, the first sound is a sample drawn from the test set, and the following are its reconstructions by the implemented models.

Model	Sample	Spectrogram	Parameters
Original preset
VAE-Flow-post
VAE-Flow
CNN
MLP
VAE
WAE

Macro-control learning

The latent dimensions can be seen as meta-parameters for the synthesizer that naturally arise from our framework. Moreover, as they act in the latent audio space, one could hope they impact audio features in a smoother way than native parameters.

The following examples present the evolution of synth parameters and corresponding spectrogram while moving along a dimension of the latent space. Spectrograms generally show a smooth variation in audio features, while parameters move in a non-independent and less smooth fashion. This proves latent dimensions rather encode audio features than simply parameters values.

Metaparameter \(z_{5}\)

Metaparameter \(z_{11}\)

Click here to see more examples

Metaparameter \(z_{6}\)

Metaparameter \(z_{8}\)

Metaparameter \(z_{9}\)

Metaparameter \(z_{15}\)

Metaparameter \(z_{16}\)

Metaparameter \(z_{19}\)

Metaparameter \(z_{20}\)

Metaparameter \(z_{24}\)

Metaparameter \(z_{25}\)

Metaparameter \(z_{26}\)

Metaparameter \(z_{28}\)

Audio space interpolation

In this experiment, we select two audio samples, and embed them in the latent space as $\mathbf{z}_0$ and $\mathbf{z}_1$. We then explore their neighborhoods, and continuously interpolate in between. At each latent point in the neighborhoods and interpolation, we are able to output the corresponding synthesizer parameters and thus to synthesize audio.

On the figure below, one can listen to the output and visualize the way spectograms and parameters evolve. It is encouraging to see how the spectrograms look alike in the neighborhoods of $\mathbf{z}_0$ and $\mathbf{z}_1$, even though parameters may vary more.

Audio	\(\mathbf{z}_0 + \mathcal{N}(0, 0.1)\)		Audio space	\(\mathbf{z}_1 + \mathcal{N}(0, 0.1)\)		Audio
	Parameters	Spectrogram		Spectrogram	Parameters
	PARAMS IMG	SPECTROGRAM	AUDIO SPACE IMG	SPECTROGRAM	PARAMS IMG
	PARAMS IMG	SPECTROGRAM		SPECTROGRAM	PARAMS IMG
	PARAMS IMG	SPECTROGRAM		SPECTROGRAM	PARAMS IMG
	PARAMS IMG	SPECTROGRAM		SPECTROGRAM	PARAMS IMG
	PARAMS IMG	SPECTROGRAM		SPECTROGRAM	PARAMS IMG

INTERPOLATION IMG

Vocal sketching

Finally, our models allow vocal sketching, by embedding a recorded vocal sample in the latent space and finding the matching parameters. Below are examples of how the models respond to several recorded samples.

Real-time implementation using Ableton Live

Not available yet.

Code

The full code will only be released after the end of the review process and will be available on the corresponding GitHub repository.